4.6. Nonlinear solvers¶

This is a collection of general-purpose nonlinear multidimensional solvers. These solvers find x for which F(x) = 0. Both x and F can be multidimensional.

4.6.1. Routines¶

Large-scale nonlinear solvers:

`newton_krylov`(F, xin[, iter, rdiff, method, ...])	Find a root of a function, using Krylov approximation for inverse Jacobian.
`anderson`(F, xin[, iter, alpha, w0, M, ...])	Find a root of a function, using (extended) Anderson mixing.

General nonlinear solvers:

`broyden1`(F, xin[, iter, alpha, ...])	Find a root of a function, using Broyden’s first Jacobian approximation.
`broyden2`(F, xin[, iter, alpha, ...])	Find a root of a function, using Broyden’s second Jacobian approximation.

Simple iterations:

`excitingmixing`(F, xin[, iter, alpha, ...])	Find a root of a function, using a tuned diagonal Jacobian approximation.
`linearmixing`(F, xin[, iter, alpha, verbose, ...])	Find a root of a function, using a scalar Jacobian approximation.
`diagbroyden`(F, xin[, iter, alpha, verbose, ...])	Find a root of a function, using diagonal Broyden Jacobian approximation.

4.6.2. Examples¶

Small problem

>>>>>> def F(x):
...    return np.cos(x) + x[::-1] - [1, 2, 3, 4]
>>> import scipy.optimize
>>> x = scipy.optimize.broyden1(F, [1,1,1,1], f_tol=1e-14)
>>> x
array([ 4.04674914,  3.91158389,  2.71791677,  1.61756251])
>>> np.cos(x) + x[::-1]
array([ 1.,  2.,  3.,  4.])

Large problem

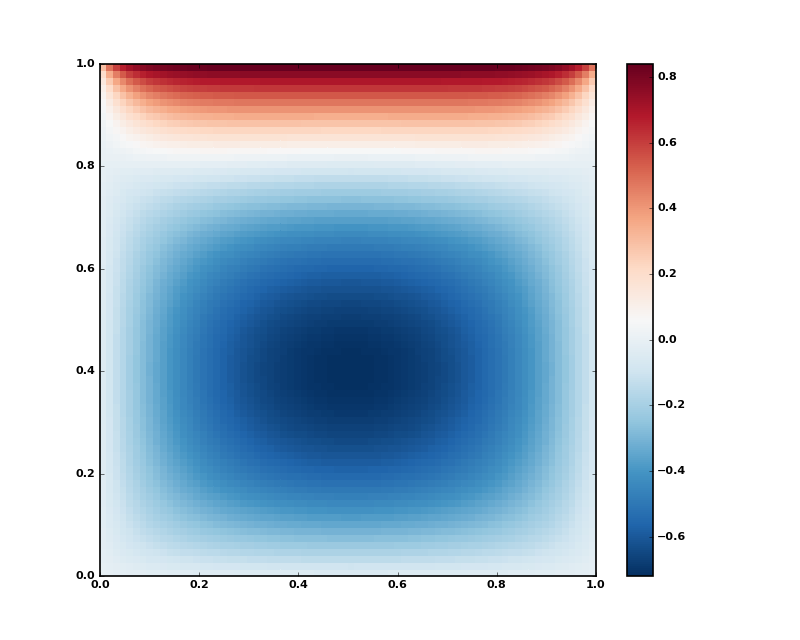
Suppose that we needed to solve the following integrodifferential equation on the square $[0,1]\times[0,1]$ :

$\nabla^2 P = 10 \left(\int_0^1\int_0^1\cosh(P)\,dx\,dy\right)^2$

with $P(x,1) = 1$ and $P=0$ elsewhere on the boundary of the square.

The solution can be found using the newton_krylov solver:

(Source code, png, hires.png, pdf)