1.12. Spatial data structures and algorithms (scipy.spatial)¶

scipy.spatial can compute triangulations, Voronoi diagrams, and convex hulls of a set of points, by leveraging the Qhull library.

Moreover, it contains KDTree implementations for nearest-neighbor point queries, and utilities for distance computations in various metrics.

1.12.1. Delaunay triangulations¶

The Delaunay triangulation is a subdivision of a set of points into a non-overlapping set of triangles, such that no point is inside the circumcircle of any triangle. In practice, such triangulations tend to avoid triangles with small angles.

Delaunay triangulation can be computed using scipy.spatial as follows:

(Source code, png, hires.png, pdf)

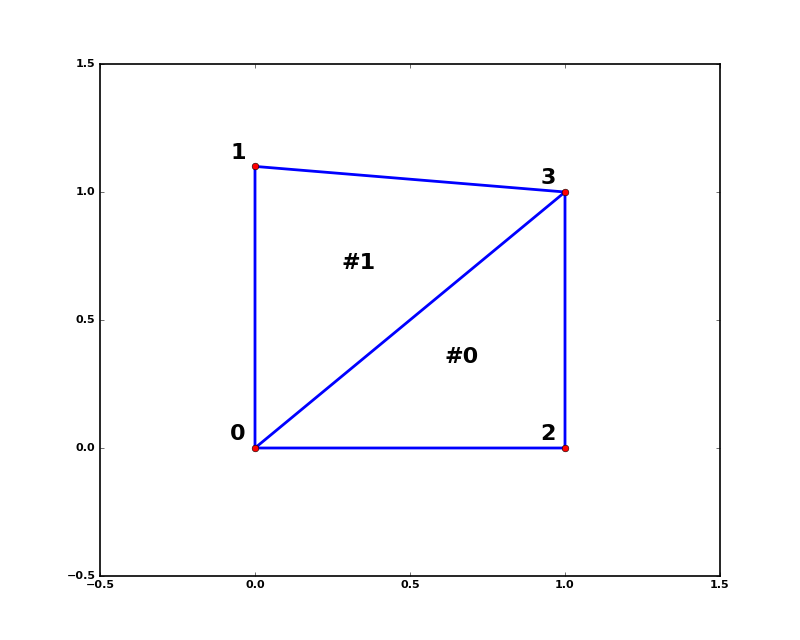
The structure of the triangulation is encoded in the following way: the simplices attribute contains the indices of the points in the points array that make up the triangle. For instance:

>>> i = 1
>>> tri.simplices[i,:]
array([3, 1, 0], dtype=int32)
>>> points[tri.simplices[i,:]]
array([[ 1. ,  1. ],
       [ 0. ,  1.1],
       [ 0. ,  0. ]])

Moreover, neighboring triangles can also be found out:

>>> tri.neighbors[i]
array([-1,  0, -1], dtype=int32)

What this tells us is that this triangle has triangle #0 as a neighbor, but no other neighbors. Moreover, it tells us that neighbor 0 is opposite the vertex 1 of the triangle:

>>> points[tri.simplices[i, 1]]
array([ 0. ,  1.1])

Indeed, from the figure we see that this is the case.

Qhull can also perform tesselations to simplices also for higher-dimensional point sets (for instance, subdivision into tetrahedra in 3-D).

1.12.1.1. Coplanar points¶

It is important to note that not all points necessarily appear as vertices of the triangulation, due to numerical precision issues in forming the triangulation. Consider the above with a duplicated point:

>>> points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
>>> tri = Delaunay(points)
>>> np.unique(tri.simplices.ravel())
array([0, 1, 2, 3], dtype=int32)

Observe that point #4, which is a duplicate, does not occur as a vertex of the triangulation. That this happened is recorded:

>>> tri.coplanar
array([[4, 0, 3]], dtype=int32)

This means that point 4 resides near triangle 0 and vertex 3, but is not included in the triangulation.

Note that such degeneracies can occur not only because of duplicated points, but also for more complicated geometrical reasons, even in point sets that at first sight seem well-behaved.

However, Qhull has the “QJ” option, which instructs it to perturb the input data randomly until degeneracies are resolved:

>>> tri = Delaunay(points, qhull_options="QJ Pp")
>>> points[tri.simplices]
array([[[1, 0],
        [1, 1],
        [0, 0]],
       [[1, 1],
        [1, 1],
        [1, 0]],
       [[1, 1],
        [0, 1],
        [0, 0]],
       [[0, 1],
        [1, 1],
        [1, 1]]])

Two new triangles appeared. However, we see that they are degenerate and have zero area.

1.12.2. Convex hulls¶

Convex hull is the smallest convex object containing all points in a given point set.

These can be computed via the Qhull wrappers in scipy.spatial as follows:

(Source code, png, hires.png, pdf)

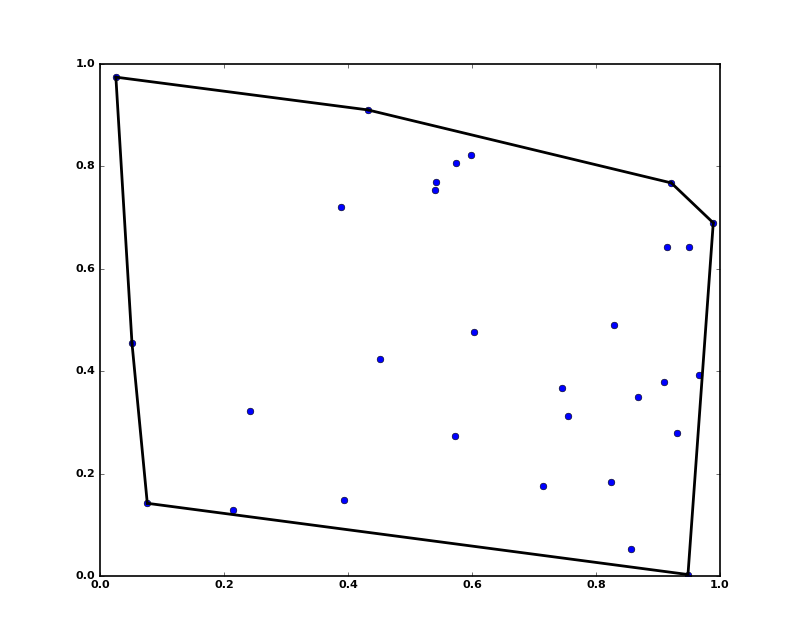
The same can be achieved with scipy.spatial.convex_hull_plot_2d.

1.12.3. Voronoi diagrams¶

A Voronoi diagram is a subdivision of the space into the nearest neighborhoods of a given set of points.

There are two ways to approach this object using scipy.spatial. First, one can use the KDTree to answer the question “which of the points is closest to this one”, and define the regions that way:

(Source code, png, hires.png, pdf)

(png, hires.png, pdf)

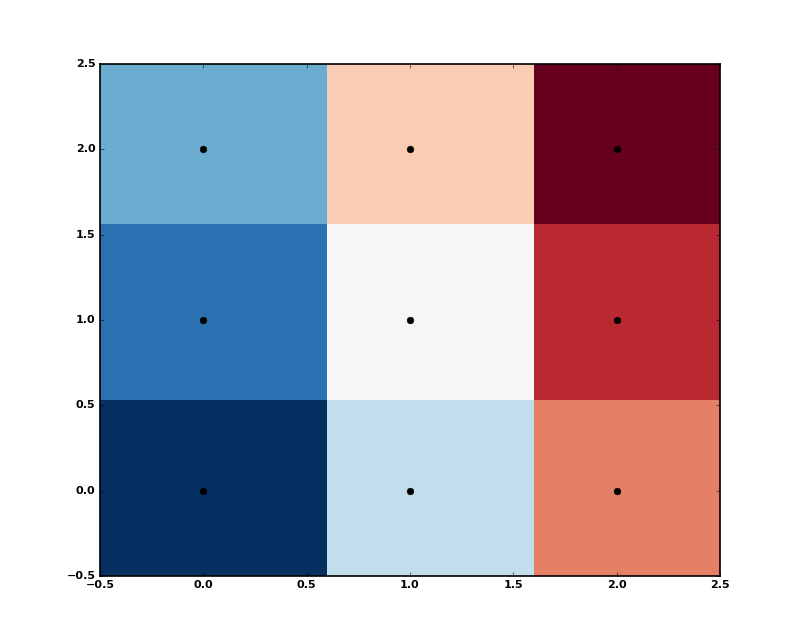
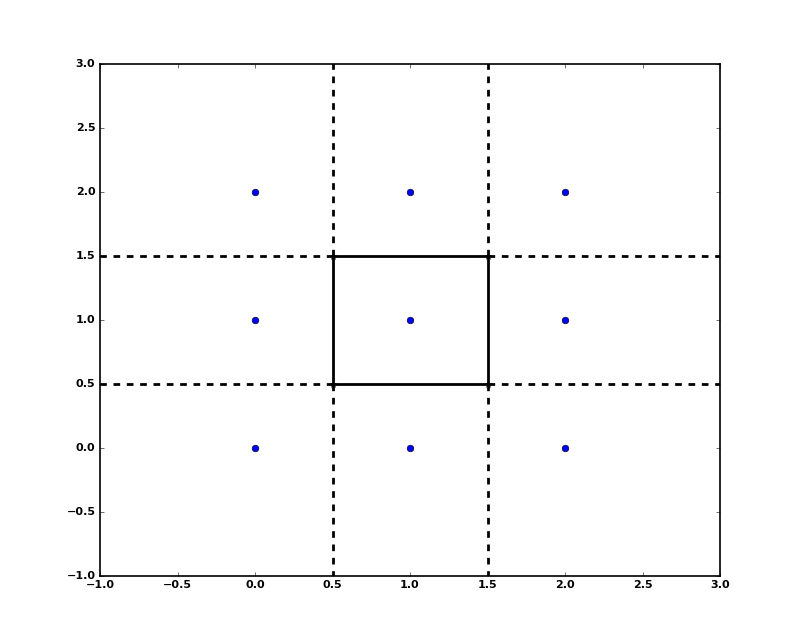
This plot can also be created using scipy.spatial.voronoi_plot_2d.