In [1]: import matplotlib as mpl

#mpl.rcParams['legend.fontsize']=20.0
#print mpl.matplotlib_fname() # location of the rc file
#print mpl.rcParams # current config
In [2]: print mpl.get_backend()
Qt5Agg

8.4 Plotting Tools

These functions can be imported from pandas.tools.plotting and take a Series or DataFrame as an argument.

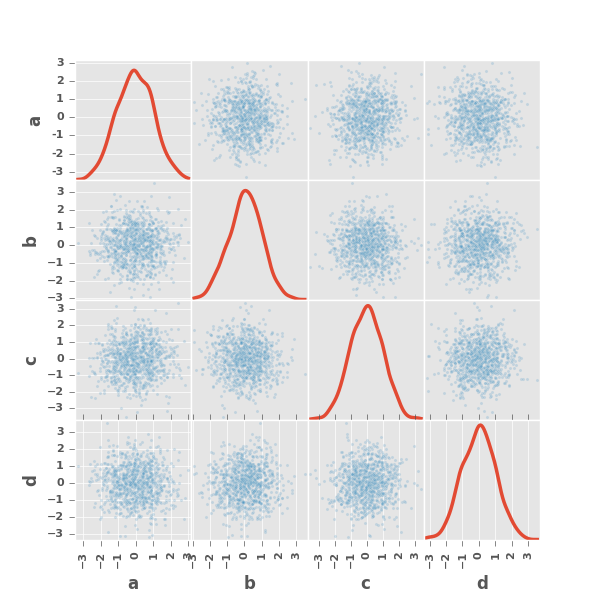
8.4.1 Scatter Matrix Plot

New in version 0.7.3.

You can create a scatter plot matrix using the scatter_matrix method in pandas.tools.plotting:

In [3]: from pandas.tools.plotting import scatter_matrix

In [4]: df = pd.DataFrame(np.random.randn(1000, 4), columns=['a', 'b', 'c', 'd'])

In [5]: scatter_matrix(df, alpha=0.2, figsize=(6, 6), diagonal='kde')
Out[5]: 
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x2b35bc919190>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35b9f3e610>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35b9d20f10>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bc2f1590>],
       [<matplotlib.axes._subplots.AxesSubplot object at 0x2b35bc700990>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bc6ac550>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bd368610>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bc71fed0>],
       [<matplotlib.axes._subplots.AxesSubplot object at 0x2b35bcc81490>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bca0e410>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bcc4c1d0>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bc935490>],
       [<matplotlib.axes._subplots.AxesSubplot object at 0x2b35bc893450>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bd3cf850>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bc9a7f10>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x2b35bc735710>]], dtype=object)
../_images/scatter_matrix_kde.png

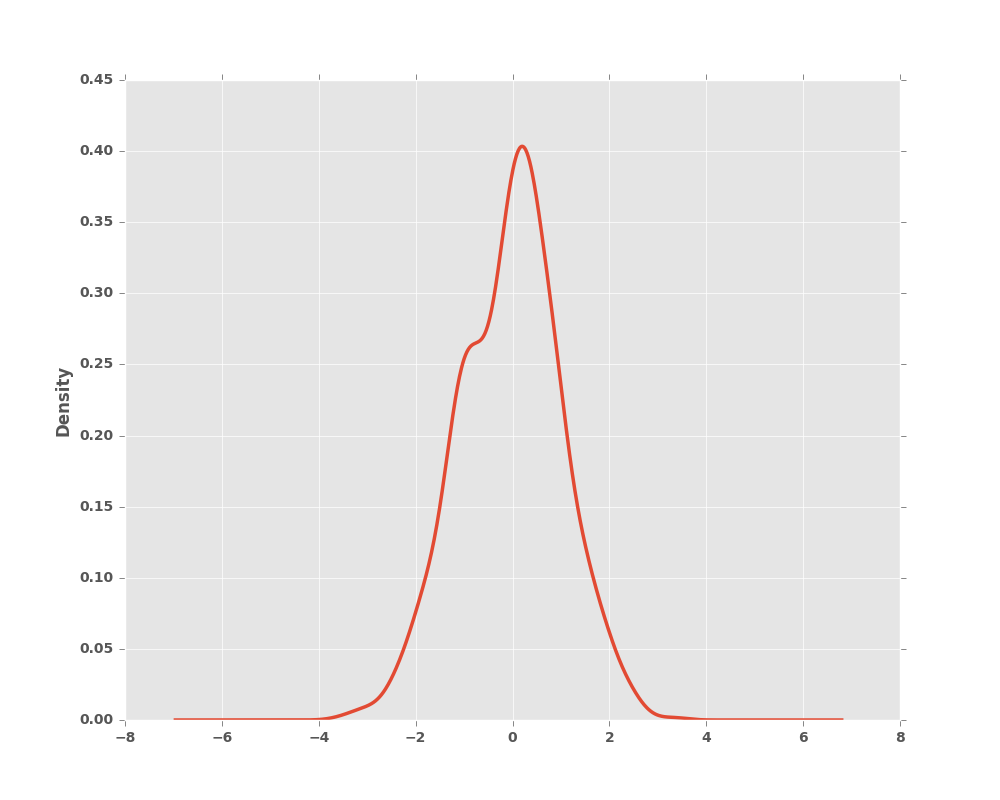
8.4.2 Density Plot

New in version 0.8.0.

You can create density plots using the Series.plot.kde() and DataFrame.plot.kde() methods.

In [6]: ser = pd.Series(np.random.randn(1000))

In [7]: ser.plot.kde()
Out[7]: <matplotlib.axes._subplots.AxesSubplot at 0x2b35bd88ac10>
../_images/kde_plot.png

8.4.3 Andrews Curves

Andrews curves allow one to plot multivariate data as a large number of curves that are created using the attributes of samples as coefficients for Fourier series. By coloring these curves differently for each class it is possible to visualize data clustering. Curves belonging to samples of the same class will usually be closer together and form larger structures.

Note: The “Iris” dataset is available here.

In [8]: from pandas.tools.plotting import andrews_curves

In [9]: url = 'https://raw.githubusercontent.com/pydata/pandas/master/doc/data/iris.data'

In [10]: data = pd.read_csv(url)

In [11]: plt.figure()
Out[11]: <matplotlib.figure.Figure at 0x2b35bdb13e90>

In [12]: andrews_curves(data, 'Name')
Out[12]: <matplotlib.axes._subplots.AxesSubplot at 0x2b35bdaa8310>
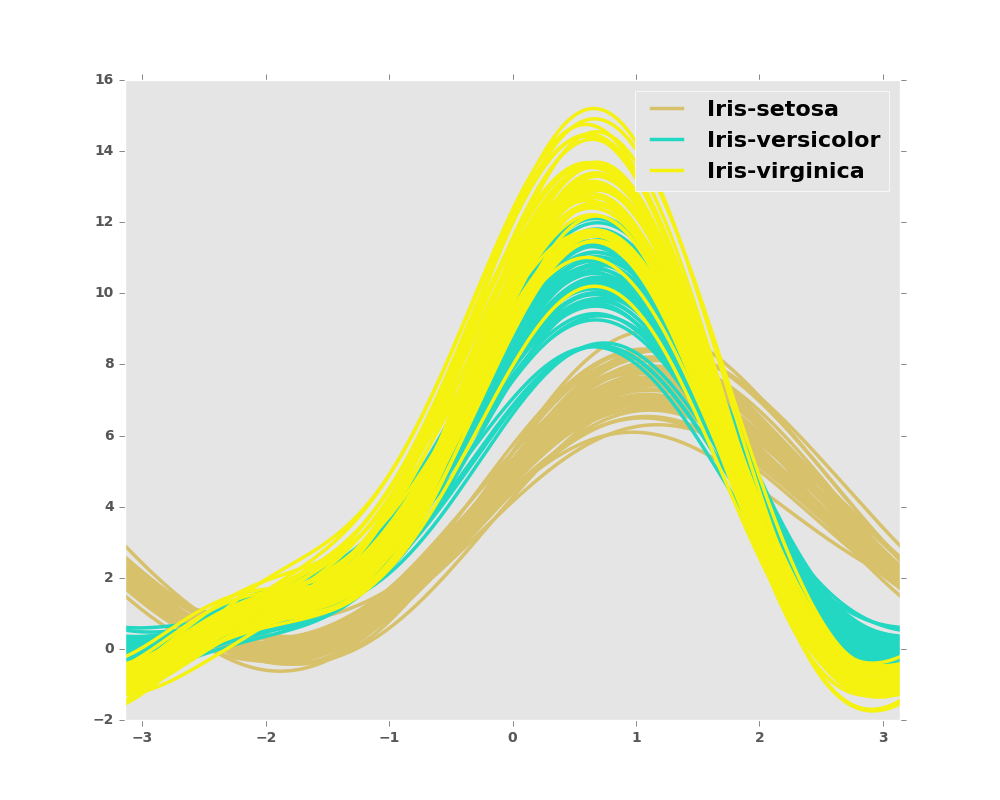
../_images/andrews_curves.png

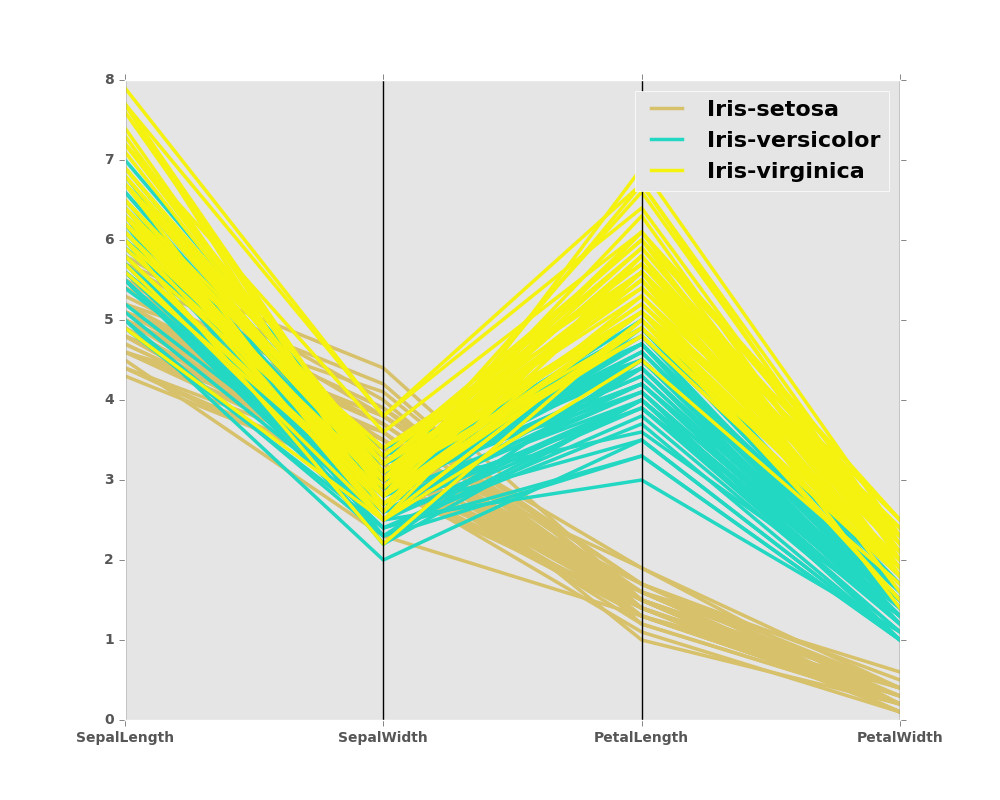
8.4.4 Parallel Coordinates

Parallel coordinates is a plotting technique for plotting multivariate data. It allows one to see clusters in data and to estimate other statistics visually. Using parallel coordinates points are represented as connected line segments. Each vertical line represents one attribute. One set of connected line segments represents one data point. Points that tend to cluster will appear closer together.

In [13]: from pandas.tools.plotting import parallel_coordinates

In [14]: data = pd.read_csv(url)

In [15]: plt.figure()
Out[15]: <matplotlib.figure.Figure at 0x2b35bdbab590>

In [16]: parallel_coordinates(data, 'Name')
Out[16]: <matplotlib.axes._subplots.AxesSubplot at 0x2b35acd80c90>
../_images/parallel_coordinates.png

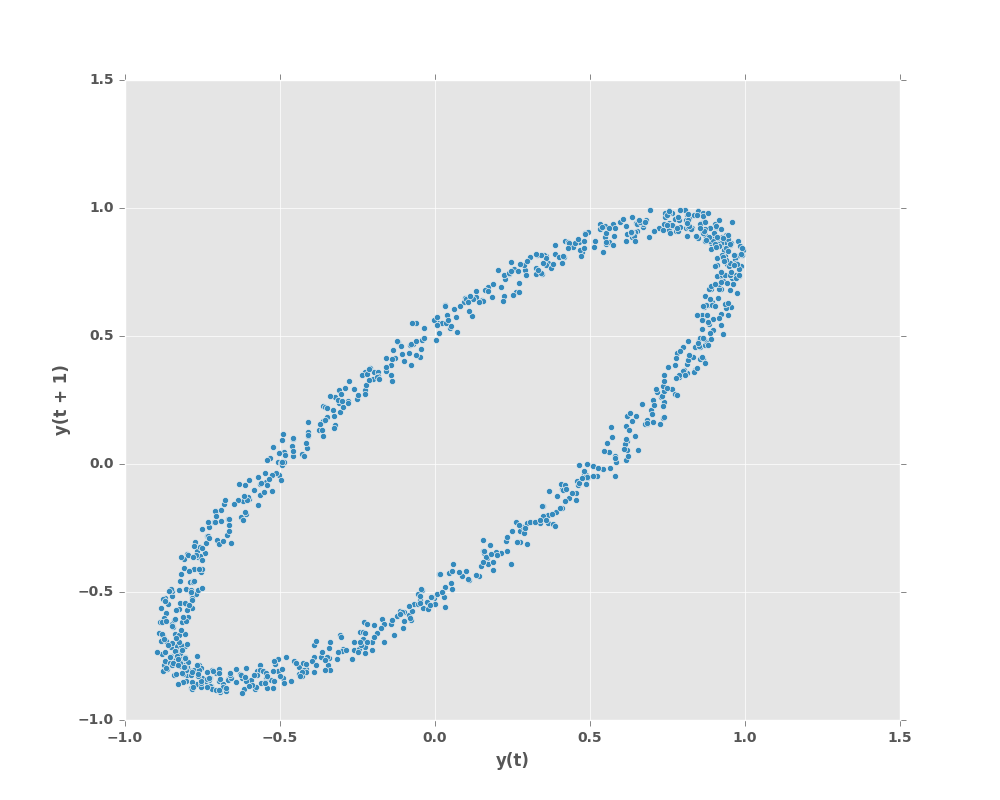
8.4.5 Lag Plot

Lag plots are used to check if a data set or time series is random. Random data should not exhibit any structure in the lag plot. Non-random structure implies that the underlying data are not random.

In [17]: from pandas.tools.plotting import lag_plot

In [18]: plt.figure()
Out[18]: <matplotlib.figure.Figure at 0x2b35bdfa4ed0>

In [19]: data = pd.Series(0.1 * np.random.rand(1000) +
   ....:     0.9 * np.sin(np.linspace(-99 * np.pi, 99 * np.pi, num=1000)))
   ....: 

In [20]: lag_plot(data)
Out[20]: <matplotlib.axes._subplots.AxesSubplot at 0x2b35be027f90>
../_images/lag_plot.png

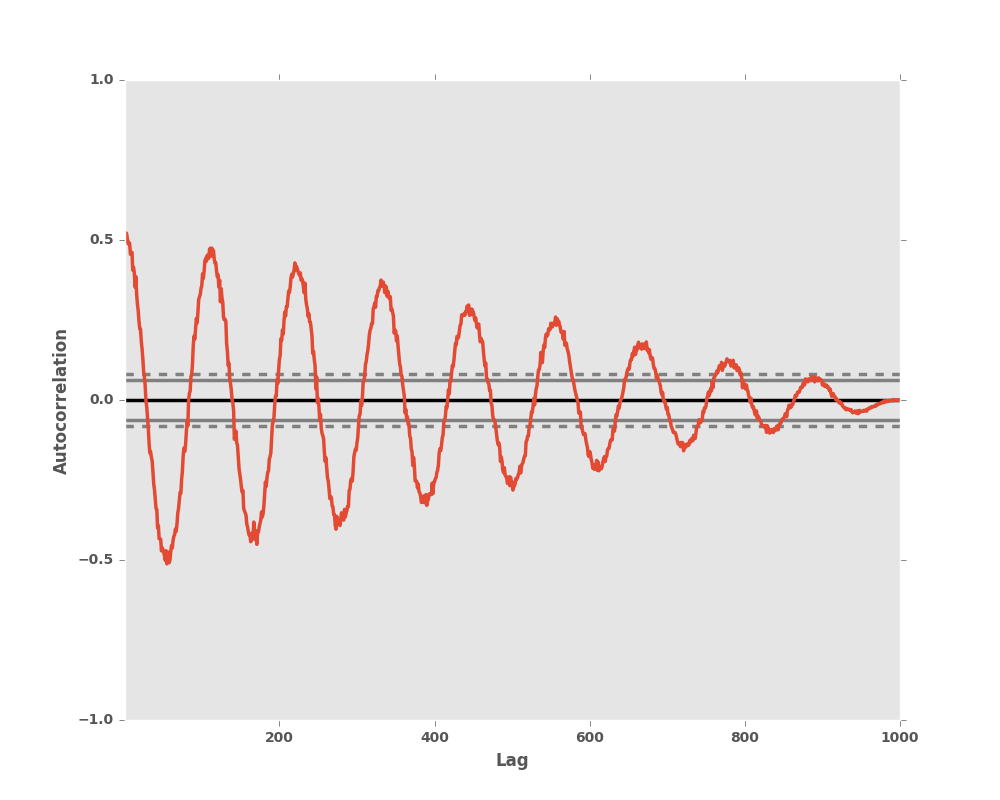
8.4.6 Autocorrelation Plot

Autocorrelation plots are often used for checking randomness in time series. This is done by computing autocorrelations for data values at varying time lags. If time series is random, such autocorrelations should be near zero for any and all time-lag separations. If time series is non-random then one or more of the autocorrelations will be significantly non-zero. The horizontal lines displayed in the plot correspond to 95% and 99% confidence bands. The dashed line is 99% confidence band.

In [21]: from pandas.tools.plotting import autocorrelation_plot

In [22]: plt.figure()
Out[22]: <matplotlib.figure.Figure at 0x2b35be07a610>

In [23]: data = pd.Series(0.7 * np.random.rand(1000) +
   ....:    0.3 * np.sin(np.linspace(-9 * np.pi, 9 * np.pi, num=1000)))
   ....: 

In [24]: autocorrelation_plot(data)
Out[24]: <matplotlib.axes._subplots.AxesSubplot at 0x2b35be084c10>
../_images/autocorrelation_plot.png

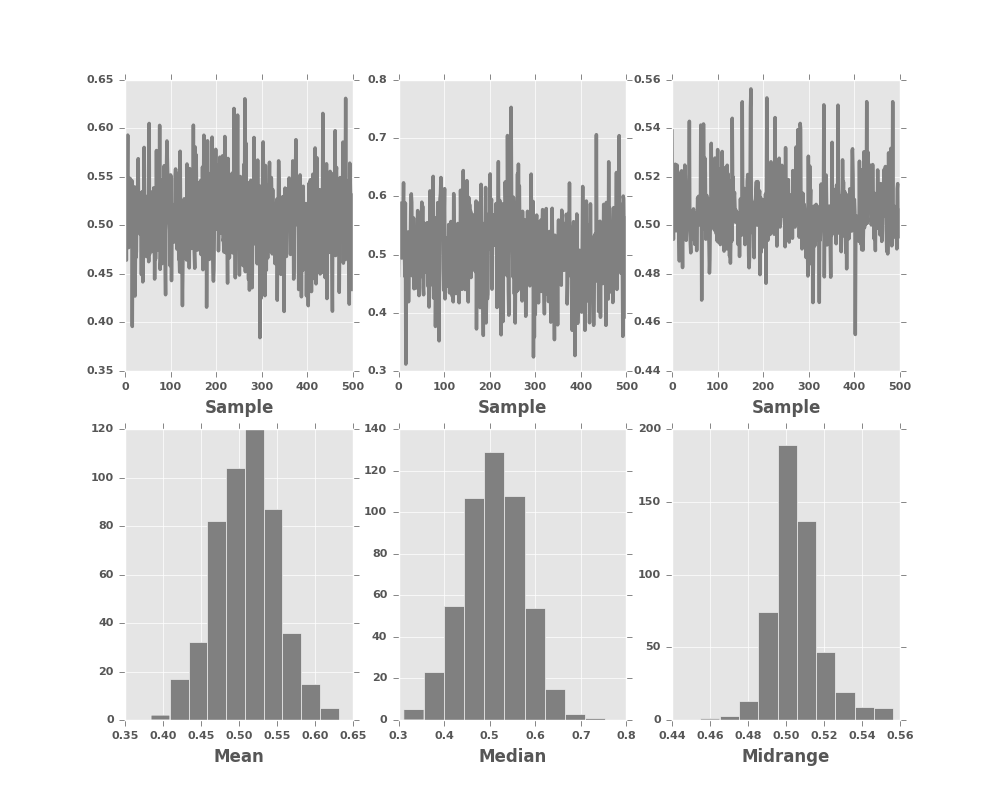
8.4.7 Bootstrap Plot

Bootstrap plots are used to visually assess the uncertainty of a statistic, such as mean, median, midrange, etc. A random subset of a specified size is selected from a data set, the statistic in question is computed for this subset and the process is repeated a specified number of times. Resulting plots and histograms are what constitutes the bootstrap plot.

In [25]: from pandas.tools.plotting import bootstrap_plot

In [26]: data = pd.Series(np.random.rand(1000))

In [27]: bootstrap_plot(data, size=50, samples=500, color='grey')
Out[27]: <matplotlib.figure.Figure at 0x2b35be05ba90>
../_images/bootstrap_plot.png

8.4.8 RadViz

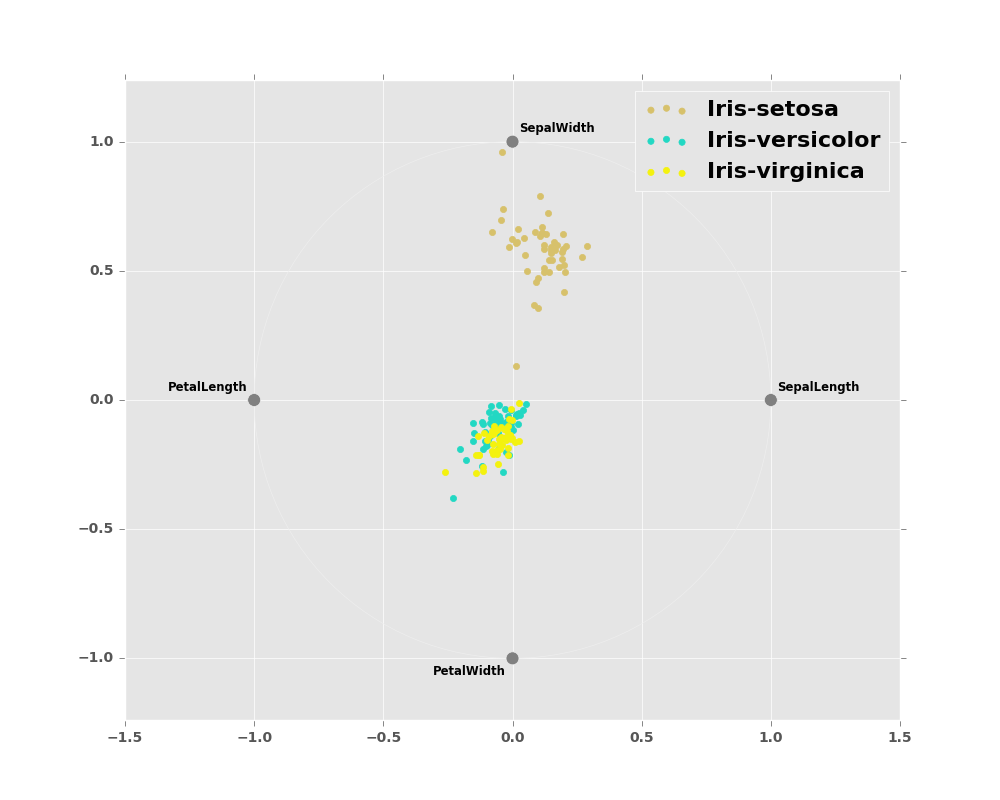
RadViz is a way of visualizing multi-variate data. It is based on a simple spring tension minimization algorithm. Basically you set up a bunch of points in a plane. In our case they are equally spaced on a unit circle. Each point represents a single attribute. You then pretend that each sample in the data set is attached to each of these points by a spring, the stiffness of which is proportional to the numerical value of that attribute (they are normalized to unit interval). The point in the plane, where our sample settles to (where the forces acting on our sample are at an equilibrium) is where a dot representing our sample will be drawn. Depending on which class that sample belongs it will be colored differently.

Note: The “Iris” dataset is available here.

In [28]: from pandas.tools.plotting import radviz

In [29]: data = pd.read_csv(url)

In [30]: plt.figure()
Out[30]: <matplotlib.figure.Figure at 0x2b35be6c0c10>

In [31]: radviz(data, 'Name')
Out[31]: <matplotlib.axes._subplots.AxesSubplot at 0x2b35be6db850>
../_images/radviz.png